Constrained DFT
This tutorial demonstrates how to perform constrained DFT (CDFT) simulations with CP2K. No previous experience with CDFT simulations is required to complete this tutorial. However, a good understanding of running DFT simulations with CP2K/QS is recommended before proceeding.
This tutorial is divided as follows. First, a brief overview of the underlying theory behind CDFT will be presented. Typical applications where CDFT simulations have been used will also be highlighted. The CDFT implementation in CP2K will then be described in detail in the next section with the aid of realistic example calculations. The last part of this tutorial covers how to calculate properties involving multiple CDFT states.
CDFT in summary
CDFT is a tool for constructing charge and/or spin localized states. Such localized states are needed in a number of applications. These include for example the following
studying charge transfer phenomena and calculating electronic couplings (e.g. using the Marcus theory approach)
correcting spurious charge delocalization due to self-interaction error
parametrizing model Hamiltonians (e.g. the Heisenberg spin Hamiltonian)
A more exhaustive list of potential applications has been presented in this review article.
The charge and spin localized states are created by enforcing electron and spin density localization within atom centered regions of space. The relevant theory has been derived by Wu and Van Voorhis in a series of key papers: paper 1, paper 2, paper 3. Further useful references can be found in the aforementioned review article. The CDFT implementation of CP2K has been throughly described in these two papers: Holmberg2017 and Holmberg2018.
In this tutorial, only the main theoretical aspects needed to understand what is happening during a CDFT simulation will be summarized. The charge/spin localized states can be generated by augmenting the Kohn-Sham energy functional, \(E_\mathrm{KS}\), by additional constraint potentials
where \(\vec\lambda = [\lambda_1, \lambda_2, \cdots]^T\) are the constraint Lagrangian multipliers (“strength(s) of the constraint potential(s)”), \(w^i(\mathbf{r})\) is an atom centered weight function, and \(N_c\) is the target value of the constraint. Multiple constraints can be included in a CDFT simulation (the sum over \(c\) above). The weight function is constructed as a normalized sum over select constraint atoms \(\mathcal{C}\)
where \(c_j\) are atomic coefficients which determine how each atom is included in the constraint (more on this later), \(P_j\) is the so-called cell function which determines the volume occupied by atom \(j\) according to some population analysis method, and \(\mathcal{N}\) is the set of all atoms in a system. Different types of constraints can be constructed by modifying the weight function according to the following conventions
charge density constraint (\(\rho^\uparrow + \rho^\downarrow\)): \(w^\uparrow = w^\downarrow = w\)
magnetization density constraint (\(\rho^\uparrow - \rho^\downarrow\)): \(w^\uparrow = -w^\downarrow = w\)
spin specific constraint (\(\rho^{\uparrow/\downarrow}\)): \(w^{\uparrow/\downarrow} = w, w^{\downarrow/\uparrow} = 0\)
The Becke and Hirshfeld space partitioning schemes can be used as constraint weight functions in CP2K. The main differences between these two constraints will be explained in a subsequent section.
When CDFT is used in a molecular dynamics or a geometry optimization simulation, additional force terms arising from the constraints are calculated
The CDFT energy expression, \(E_\mathrm{CDFT}\), is solved self-consistently using a two-tiered approach: one external optimization loop for the constraints, and an inner loop to converge the electronic structure. In practice, three SCF loops are needed to integrate CDFT with the OT method, which uses its own outer loop to reset the OT preconditioner. This process has been schematically illustrated in Figure 1.
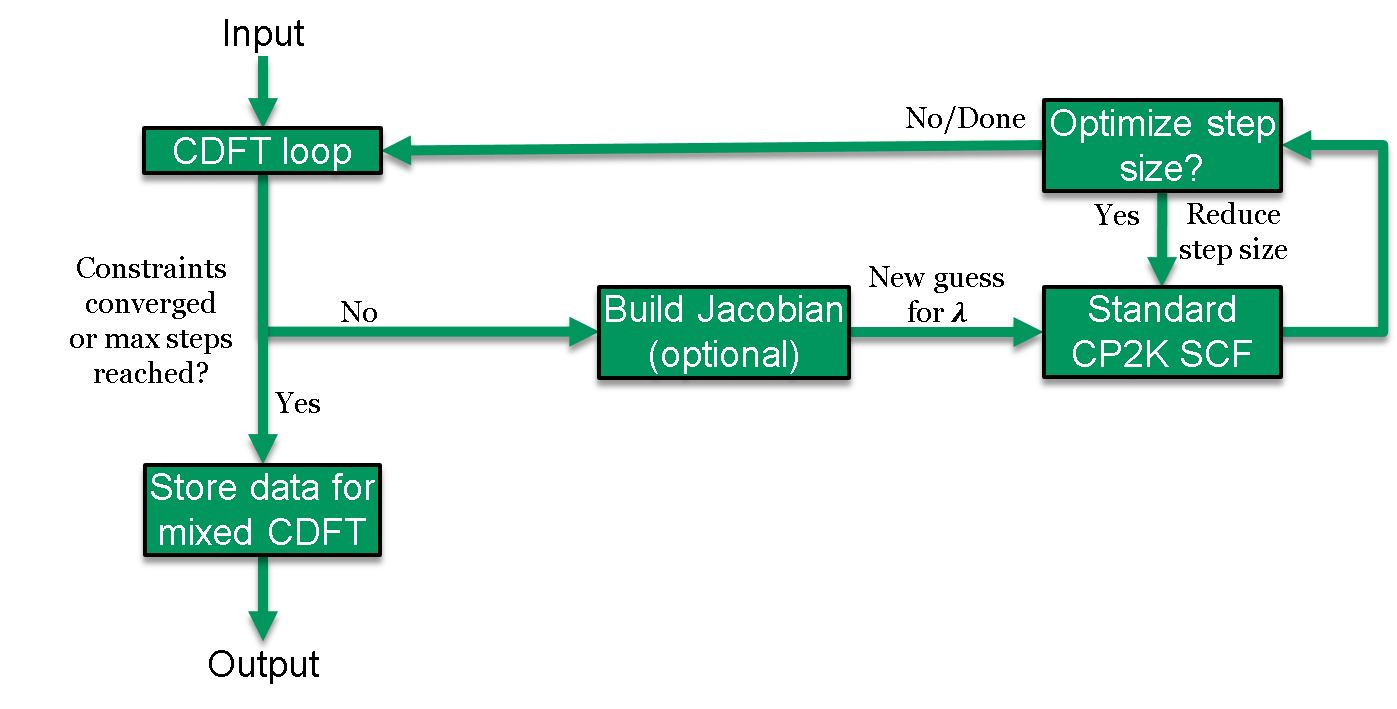
Figure 1. Schematic of the CDFT SCF procedure. The constraint Lagrangians \(\vec\lambda\) are first optimized in the outer CDFT loop, their values are subsequently fixed, and the electron density corresponding to these fixed values is solved like in traditional CP2K DFT simulations. The control is then returned to the outer CDFT loop where convergence of the constraints is checked. This iteration process is repeated until convergence is achieved or until the number of maximum CDFT SCF steps is reached. The structure of the CDFT loop will be further described below.
By definition, all constraints are satisfied when
The constraint Lagrangian multipliers \(\vec\lambda\) can therefore be optimized by minimizing the constraint error expression \(\max |\vec c(\vec\lambda)|\) until the largest element decreases below a threshold \(\varepsilon\). Root-finding algorithms are used to optimize \(\lambda\). For Newton and quasi-Newton class optimizers, a new guess for \(\vec\lambda\) at step \(n\) is generated according to the following iteration formula
where \(\alpha \in (0, 1]\) is the step size and \(\mathbf{J}^{-1}\) is the inverse Jacobian matrix. The step size \(\alpha\) can be fixed or its value can be optimized with backtracking line search, where the value of \(\lambda\) is successively reduced if it decreases the constraint error function. The Jacobian matrix is approximated with finite differences, e.g. using a first order forward difference stencil, by perturbing each element of \(\vec\lambda\) slightly and re-evaluating the value of \(\vec c\) self-consistently (an SCF energy optimization)
where \(\vec\delta_j\) is a small perturbation of the \(j\)th component of \(\vec\lambda\).
Using the CDFT module
The input section CDFT is used to set up a CDFT simulation. A brief description of this input section will be given in the next two subsections. Subsequently, various aspects of running CDFT simulations will be explored through example calculations.
Defining CDFT SCF parameters
Settings for the CDFT SCF loop are controlled by the input section CDFT. An example of a typical CDFT input is given below. These parameter selections should be suitable for most systems.
&QS
...
! CDFT loop settings
! Please note that prior to CP2K version 7.0,
! Becke constraints were separate from the CDFT section
&CDFT
TYPE_OF_CONSTRAINT BECKE
! Compute CDFT charges?
ATOMIC_CHARGES TRUE
! Constraint strength and target values
! Give one value per constraint
STRENGTH ${BECKE_STR}
TARGET ${BECKE_TARGET}
! Constraint definitions, each repetition defines a new constraint
&ATOM_GROUP
ATOMS 1
COEFF 1
CONSTRAINT_TYPE CHARGE
&END ATOM_GROUP
! No constraint applied but calculate charges
&DUMMY_ATOMS
ATOMS 2
&END DUMMY_ATOMS
! CDFT convergence and optimizer settings
&OUTER_SCF ON
TYPE CDFT_CONSTRAINT
EXTRAPOLATION_ORDER 2
MAX_SCF 10
! Convergence threshold
EPS_SCF 1.0E-3
! Optimizer selection:
! Now Newton's method with backtracking line search
OPTIMIZER NEWTON_LS
! Optimizer (initial) step size
STEP_SIZE -1.0
! Note that the section CDFT_OPT exists in CP2K version >= 6.1
! Remove section for CP2K version 5.1 (keywords are unchanged)
&CDFT_OPT ON
! Line search settings
MAX_LS 5
CONTINUE_LS
FACTOR_LS 0.5
! Finite difference settings for Jacobian matrix
JACOBIAN_STEP 1.0E-2
JACOBIAN_FREQ 1 1
JACOBIAN_TYPE FD1
JACOBIAN_RESTART FALSE
&END CDFT_OPT
&END
! Settigs specific to Becke constraints
&BECKE_CONSTRAINT
...
&END BECKE_CONSTRAINT
! Print information about CDFT calculation
&PROGRAM_RUN_INFO ON
&EACH
QS_SCF 1
&END EACH
COMMON_ITERATION_LEVELS 2
ADD_LAST NUMERIC
FILENAME ./${NAME}
&END PROGRAM_RUN_INFO
&END CDFT
&END QS
The structure of this input section is quite straightforward and consists of three parts:
Constraint definitions (type, which atoms to include, constraint target, etc)
CDFT SCF loop settings (solver, convergence criterion, etc)
Constraint weight function specific settings (Becke/Hirshfeld subsections)
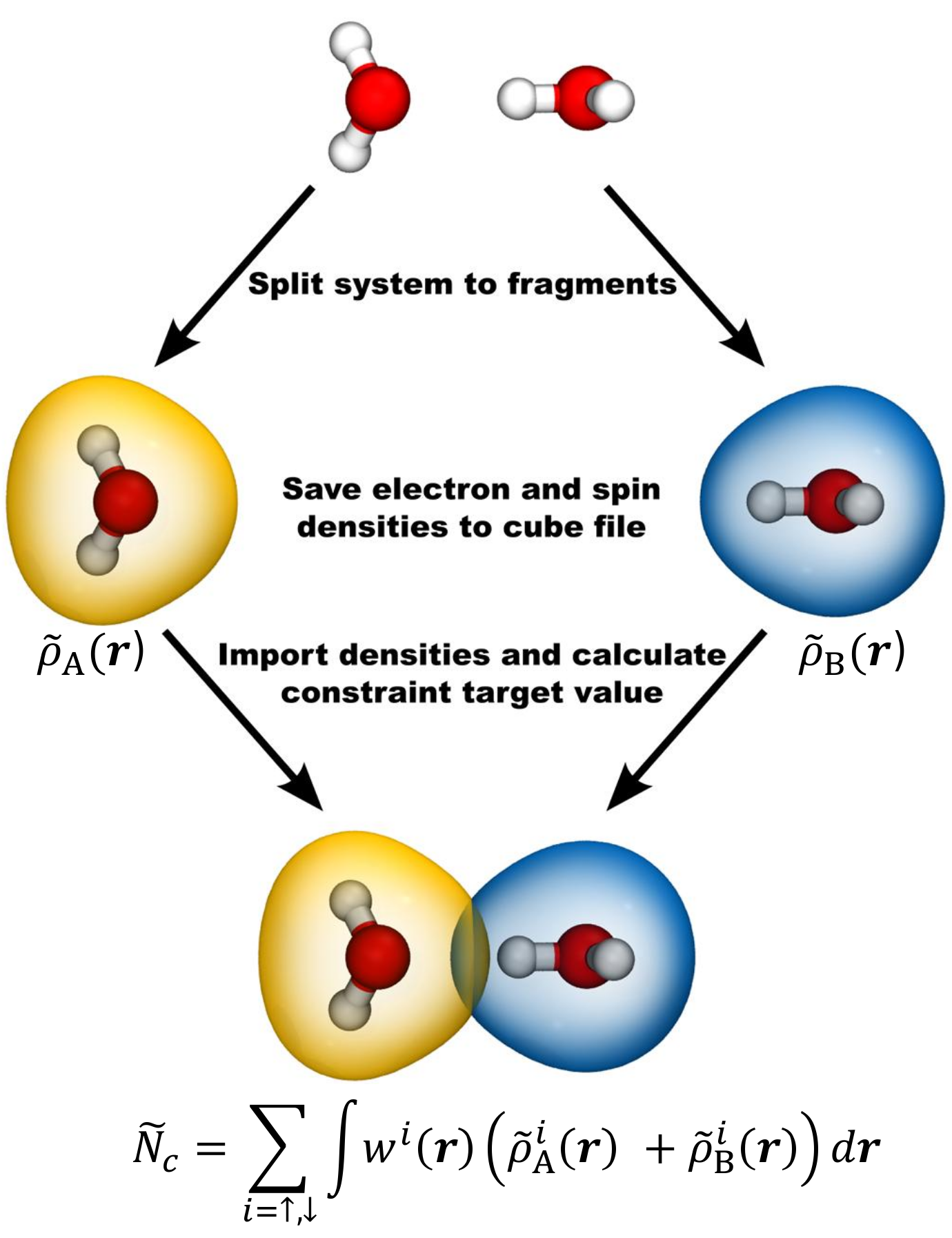
In the above example, a Becke constraint is selected using the keyword TYPE_OF_CONSTRAINT. The actual constraints are defined using the section ATOM_GROUP. Each repetition of this section defines a new constraint. The constraint atoms are selected with the keyword ATOMS and the keyword COEFF determines how the atoms are summed up to form the constraint. Usually all coefficients are set to +1, but mixing +1 and -1 coefficients would define the constraint as the difference between two groups of atoms. The keywords TARGET and STRENGTH define the constraint target values and the initial constraint strengths \(\vec\lambda\), respectively. The constraint target value should be the desired number of valence electrons on the constraint atoms, suitably multiplied by atomic coefficients in case a relative constraint between two atom groups has been used. The constaint type is selected with the keyword CONSTRAINT_TYPE. It is also possible to use fragment based constraints FRAGMENT_CONSTRAINT, in which case the constraint target value is calculated from the superposition of isolated fragment densities according to the scheme in Figure 2.
Figure 2. Using a fragment based CDFT constraint. The system is first divided into two fragments with atomic positions fixed in the same configuration as in the full system. The electron and spin densities of the fragment systems are then saved to cube files and subsequently used as input files for the CDFT calculation, where the constraint target value is calculated from the superimposed fragment densities.
The OUTER_SCF section within the CDFT section defines settings for the CDFT SCF loop. The keyword
EPS_SCF defines the CDFT constraint
convergence threshold \(\varepsilon\) and
OPTIMIZER selects the CDFT optimizer.
Using Newton or quasi-Newton optimizers (Broyden methods) is recommended for most applications.
These optimizers accept additional control settings that define how the Jacobian matrix is
calculated (keywords JACOBIAN_*) and how to optimize the step size \(\alpha\) (keywords *_LS).
These keywords are available in the
CDFT_OPT section. MD simulations with a
single constraint might benefit from using the bisect optimizer, which avoids building the Jacobian
matrix, in case a considerable amount of the total time per MD step is spent in building the
Jacobian. Notice, however, that the frequency of Jacobian rebuilds
JACOBIAN_FREQ can be
controlled on a per MD step and per CDFT SCF step basis. The Broyden optimizers require less
frequent rebuilds of the Jacobian matrix because the matrix is
rank-one updated every iteration, although the
stability of the method with respect to the rebuild frequency needs to be carefully studied.
Above, for instance, the Jacobian is explicitly calculated every CDFT SCF iteration and MD step by perturbing each constraint Lagragian using a first order forward difference stencil with a step size of \(10^{-2}\). The Newton step size is optimized with backtracking line search using the update formula \(\alpha_n = 0.5*\alpha_{n-1}\) for a maximum of 5 steps as long as the CDFT constraint error decreases.
Available constraints
The CDFT module in CP2K currently supports using Becke or Hirshfeld based constraints. The main aspects of these weight functions and their use as CDFT constraints will be explained in this section. Weight function specific settings are defined in the sections BECKE_CONSTRAINT HIRSHFELD_CONSTRAINT. If you want to visualize the weight functions to e.g. see the effects of using different parameters, you can use the section WEIGHT_FUNCTION to print the CDFT weight function to a cube file.
Becke constraints
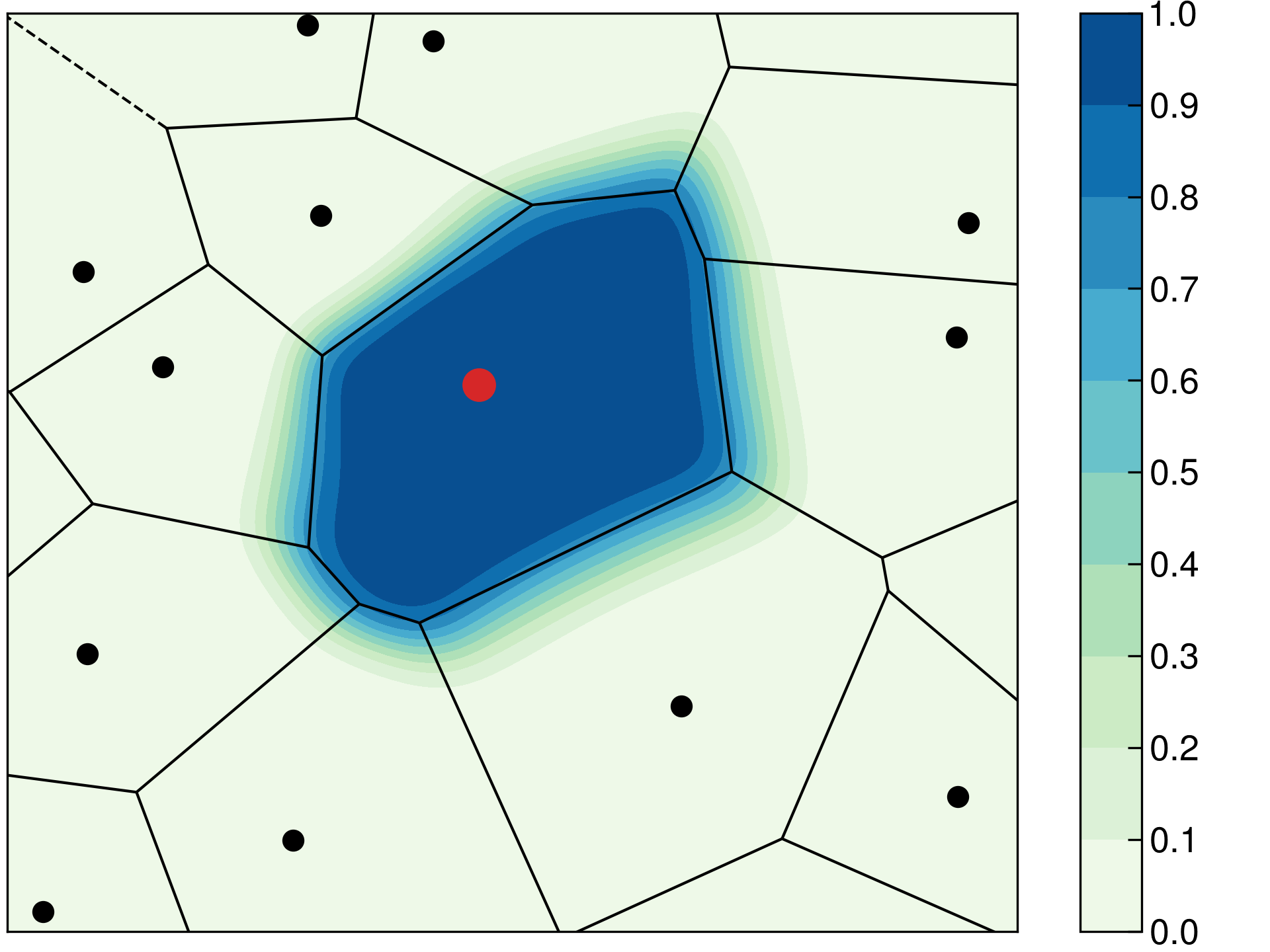
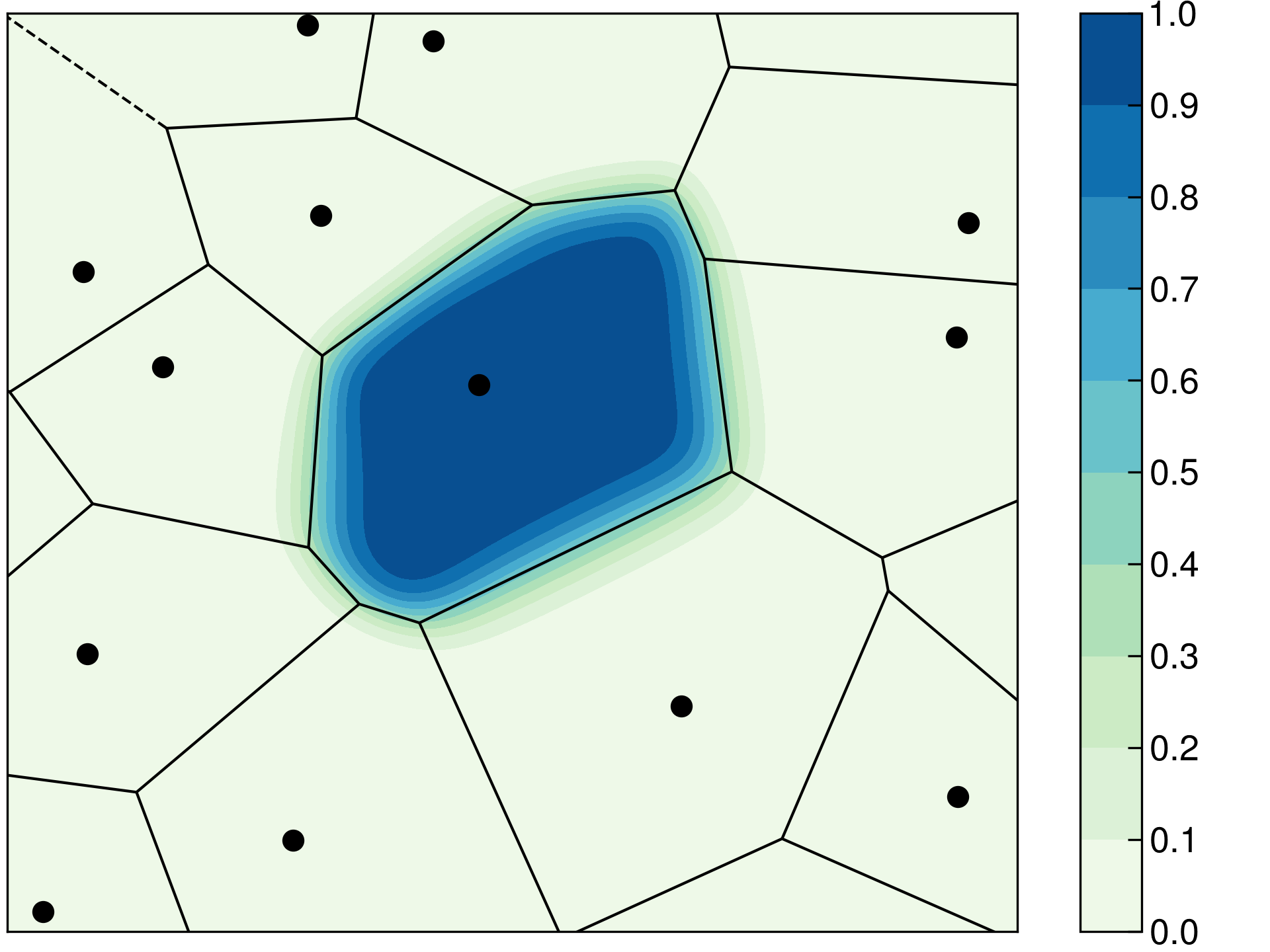
The Becke density partitioning method can be considered as a smoothed Voronoi scheme. In Voronoi partitioning, the volume occupied by each atom is the set of real space grid points \(\mathbf{r}\) which are closer to that particular atom than to any other atom in the system. An example Voronoi diagram is given below in Figure 3. The line segments in this figure define real space points which are equidistant from two atoms, while vertices correspond to grid points which are equidistant from three or more atoms. The Becke cell function \(P_i\) is overlayed on top of the Voronoi diagram and it decays smoothly from 1 to 0 across the Voronoi polyhedron boundary. Using a smooth density partitioning function improves numerical stability in simulations.
Figure 3. Comparison of the Voronoi (lines) and Becke partitioning (contours) schemes. At left, the Becke partitioning is performed without atomic size information. At right, the size of the red atom is 30 % larger than the black atoms, and the contours of the red atom extend farther than without atomic size adjustments.
The Voronoi and, by extension, the Becke partitioning methods treat each element equally. This leads to unphysical partial charges in most systems. For example, the Becke scheme predicts a positive charge on oxygen and a negative charge on hydrogen in water (see examples for input files). This problem can be remedied by accounting for atomic radii during the partitioning. This behavior is activated by the keyword ADJUST_SIZE and the atomic radii are defined with the keyword ATOMIC_RADII. The atomic radii should be set to values that reflect the system under simulation, e.g. using additive covalent radii for covalent molecules or Shannon’s ionic radii for ionic compounds. An example on how atomic size adjustments affect the Becke cell functions has been visualized above in Figure 3 at right, where the size of the red atom is set to a value 30 % larger than the black atoms causing the red atom’s contours to extend farther than without atomic size adjustments.
The algorithmic implementation of the Becke density partitioning method has been detailed in
Holmberg2017. In brief, this involves iterating over each atom pair permutation
\(\{\mathbf{R}_i, \mathbf{R}_j\}, j\neq i\) at every real space grid point \(\mathbf{r}\). This leads to
a poor scaling with respect to the system size (cell size and planewave cutoff) and the number of
atoms within the system, and is particularly troublesome for solvated system simulations. The
computational cost of the Becke method can be considerably decreased by noting that only the grid
points within a cutoff distance \(R_{cutoff}\)
(CUTOFF_TYPE) of atoms involved
in constraints actually need to be considered. The other grid points can be efficiently screened
with constraint atom centered spherical Gaussian functions, activated by the keyword
CAVITY_CONFINE and controlled
by other keywords of the form CAVITY_*. The exact details of this confinement scheme and why it
can be used are explained in the implementation paper.
An example of a Becke constraint input section is given below. This choice of parameters should be reasonable for most systems, ignoring the atomic radii and constraint definitions which are system dependent. Decreasing the partitioning cutoff might be useful for solvated system MD simulations, but extensive testing is always necessary before starting production simulations.
&CDFT
...
&BECKE_CONSTRAINT
! Take atomic radii into account?
ADJUST_SIZE FALSE
ATOMIC_RADII 0.63 0.32
! Cutoff scheme
CUTOFF_TYPE ELEMENT
ELEMENT_CUTOFF 6.0
! Perform Becke partitioning only within the space
! spanned by constraint atom centered spherical Gaussians
! (reduces cost for solvated systems)
CAVITY_CONFINE TRUE
CAVITY_SHAPE VDW
EPS_CAVITY 1.0E-7
IN_MEMORY TRUE
SHOULD_SKIP TRUE
&END CDFT
Hirshfeld constraints
Hirshfeld constraints are cheaper to construct than Becke constraints in large systems because Hirshfeld constraints are essentially just weighted sums of spherical Gaussian functions. The keywords SHAPE_FUNCTION and GAUSSIAN_SHAPE define which type of Hirshfeld constraint to apply to the system, consistent with the options for printing of Hirshfeld atomic charges (see SHAPE_FUNCTION).
The shape function keyword accepts two values: Gaussian or Density.
The first choice implies that the CDFT weight function for each atom is a single Gaussian function whose radius is controlled by the GAUSSIAN_SHAPE keyword. By default, tabulated covalent radii are used as the radii of the Gaussian, but it is also possible to select van der Waals radii or to define custom radii.
The latter choice implies that the atomic weight function are constructed from isolated atomic densities which are expanded in terms of multiple spherical Gaussians. This choice avoids the introduction of any empirical parameters, and generally provides a more robust description of atomic charges than either Becke or Gaussian based Hirshfeld charge partitioning.
Selected examples
Zn dimer cation
In this example, we will perform two CDFT simulations for the Zn dimer cation \(\mathrm{Zn}_2^+\). As the distance \(R\) between the two atoms is increased, the excess charge in the system should localize onto one of the Zn atoms forming \(\mathrm{Zn}^+ + \mathrm{Zn}\). With standard GGA and hybrid functionals, such as PBE, PBE0, BLYP or B3LYP, this is however not the case. The excess charge will instead be equally shared among the two atoms \(\mathrm{Zn}^{0.5+} + \mathrm{Zn}^{0.5+}\) regardless of separation. We can force the charge to localize onto one of these atoms with CDFT.
You can download the input files from
here. Unzip the folder and execute the
file energy.bash (use flag -h for usage instructions) to run a standard DFT calculation,
followed by two CDFT simulations where the first Zn atom is constrained to charges +1 and 0,
respectively. The script will also run a mixed CDFT calculation, which will be analyzed in a
subsequent section. Modify paths to basis sets and other CP2K
data files in the file dft-common-params.inc in case they are in non-standard paths relative to
the CP2K binary. The calculations will take a while to run. In the meanwhile, you can
Check the calculated partial charges in the standard DFT output file
Study the script file to understand how it works
Study the generated output files from the CDFT simulations
Assuming the CDFT simulations have finished, the following files were generated
*.outThis is the standard CP2K output file and now also contains all the output from the CDFT SCF iterations. Each iteration step starts a new DFT energy optimization using new values of the constraint Lagrangian multipliers \(\vec{\lambda}\), as generated by the selected CDFT optimizer.
An example output from the end of one the CDFT simulations is provided below.
Information about the CDFT SCF iteration process and the constraints and their convergence is printed alongside the usual CP2K SCF iteration information.
With CDFT optimizers that support backtracking line search, the density optimization process at each CDFT SCF step is restarted from the optimized constraint strength and density obtained previously during line search. Consequently, when the line search was successful (i.e. the energy optimization converged), the density optimization should converge terminate in exactly 1 step each CDFT SCF iteration (refer to the output files, as this should now be the case).
*-LineSearch.outThe progress of the optimization of the Newton step size \(\alpha\) using backtracking line search is reported in this file. Observe that the step size is halved on each iteration if the CDFT constraint error (“Deviation from target” in the output) decreases.
*.cdftLogCDFT parameters (atomic radii, constraint definitions and cutoffs) and Becke partial charges are printed in these files.
*-JacobianInfo.outThe output from the calculation of the Jacobian matrix \(\mathbf{J}\) is reported in this file.
*.inverseJacobianThis is a restart file for the inverse Jacobian matrix.
Using the above list, study the generated output files to understand how the CDFT SCF loop is integrated with the standard CP2K DFT SCF process.
SCF WAVEFUNCTION OPTIMIZATION
----------------------------------- OT ---------------------------------------
Minimizer : DIIS : direct inversion
in the iterative subspace
using 7 DIIS vectors
safer DIIS on
Preconditioner : FULL_ALL : diagonalization, state selective
Precond_solver : DEFAULT
stepsize : 0.15000000 energy_gap : 0.08000000
ortho_irac : CHOL irac_degree : 4
max_irac : 50 eps_irac : 0.10000E-09
eps_irac_switch: 0.10000E-01 eps_irac_quick_exit: 0.10000E-04
on_the_fly_loc : F
----------------------------------- OT ---------------------------------------
Step Update method Time Convergence Total energy Change
------------------------------------------------------------------------------
qs_ot_get_orbitals_ref 0: ||P-I||= 0.10493E-10, ortho_irac = POLY
qs_ot_ref_poly 1: quick exit!
qs_ot_get_orbitals_ref 0: ||P-I||= 0.11959E-12, ortho_irac = POLY
qs_ot_ref_poly 1: quick exit!
1 OT DIIS 0.15E+00 2.5 0.00000022 -120.6126709217 -1.21E+02
*** SCF run converged in 1 steps ***
Electronic density on regular grids: -22.9999999253 0.0000000747
Core density on regular grids: 24.0000000000 -0.0000000000
Total charge density on r-space grids: 1.0000000746
Total charge density g-space grids: 1.0000000746
Overlap energy of the core charge distribution: 0.00000000000000
Self energy of the core charge distribution: -159.30058829583706
Core Hamiltonian energy: 50.63132167014943
Hartree energy: 5.66516329750697
Exchange-correlation energy: -17.60803221234604
Dispersion energy: -0.00058223840320
Total energy: -120.61267092172808
outer SCF iter = 1 RMS gradient = 0.22E-06 energy = -120.6126709217
outer SCF loop converged in 1 iterations or 1 steps
CDFT SCF iter = 5 RMS gradient = 0.13E-03 energy = -120.6126709217
CDFT SCF loop converged in 5 iterations or 37 steps
--------------------- Becke constraint information ---------------------
Atomic group : 1
Type of constraint : Charge density constraint
Target value of constraint : 11.000000000000
Current value of constraint : 11.000126158558
Deviation from target : 1.262E-04
Strength of constraint : 0.371415167271
------------------------------------------------------------------------
Charge transfer energy in water dimer
In this example, we will calculate the charge transfer energy, \(-\Delta E_\mathrm{CT}\), of water dimer. This quantity is conveniently defined in CDFT as (see here)
where \(E_\mathrm{DFT}\) is the DFT total energy of the system, and \(E_\mathrm{CDFT}\) is the CDFT energy of the system when charge transfer between the two molecules is prevented.
We will calculate the charge transfer energy with four different constraints: default Becke
constraint, Becke constraint with atomic size adjustments using covalent radii from
this publication, and a fragment based Becke constraint
with and without the same atomic size adjustments. The input files can be downloaded from
here. Execute the file energy.bash
to run all the simulations: standard DFT simulations for the full and two fragment systems, and the
aforementioned CDFT simulations with different constraints. Modify the include (.inc) file if
necessary as you would have before. Study the input files while the calculations are running.
After the calculations have finished, answer the following questions
Compare the partial charges of unconstrained PBE water as predicted by the Becke population analysis method with and without atomic size adjustments (Hint: the CDFT calculations were restarted from the DFT wavefunction)
How much charge is transferred between the two water molecules according to the different constraint methods? Note that net charges for fragment based constraints are not reported with respect to the core charge, but they can be recovered by post-processing the reported absolute populations. Instead, each atomic charge is referenced to the number of electrons per atom in the system where the isolated densities are superimposed.
Compare the calculated charge transfer energies to the reference value 1.7 mHa, calculated at the PBE0/def-QZVP/CDFT level of theory using a different code and constraint. Which is closest to the reference value? Why? (Hint: Look at previous question)
Zn dimer cation with Hirshfeld constraints
This tutorial is exactly the same as the Zn dimer example above but using Hirshfeld partitioning based constraints instead of Becke constraints. You can find the input files here.
It might be instructive to visualize how the Becke and Hirshfeld weight function schemes differ, in particular, how the methods assign a volume to each atom in the system. You can activate the section WEIGHT_FUNCTION to output the weight function as a cube file which you can visualize with e.g. VMD. Feel free to modify the water tutorial above to look at the differences between Becke and Hirshfeld constraints in a system with different chemical elements.
Using the mixed CDFT module
Additional properties can be calculated from the interactions between CDFT states. In CP2K, these types of simulations are called mixed CDFT simulations because the module leverages the MIXED FORCE_EVAL type to efficiently treat multiple CDFT states in parallel. Mixed CDFT calculations are useful in a number of applications including
Calculating charge transfer kinetics parameters
Performing configuration interaction calculations within the basis of CDFT states
In this part of the tutorial, the theoretical basis for mixed CDFT will first be established. The quantities accessible through such simulations will also be introduced. The structure of a mixed CDFT input file will then be discussed. The tutorial is concluded with a walk through of an example calculation.
Theoretical basis
The theoretical concepts related to mixed CDFT calculations are best introduced through an example.
Consider the following one electron transfer processs
where \(\Delta A\) is the reaction free energy, \(\xi\) is the solvent reorganization energy, and \(\left|\mathbf{H}_\mathrm{ab}\right|\) is the electronic coupling. The first two quantities can be obtained from free energy simulations as discussed e.g. in Holmberg2017. The electronic coupling is rigorously defined as the interaction energy between wavefunctions \(\Psi\) representing the two reaction states
where \(\mathcal{H}\) is the many-electron Hamiltonian operator. The usefulness of the electronic coupling quantity is not limited to the Marcus rate equation, but it also a central quantity in other charge transfer theories as well as in CDFT based configuration interaction.
The true, interacting many-electron wavefunctions or the Hamiltonian are not available in CDFT simulations. The electronic coupling is instead approximated using the CDFT surrogates
where \(\Phi\) are the CDFT Kohn-Sham determinants, \(S_\mathrm{AB}= \left<\Phi_\mathrm{A}|\Phi_\mathrm{B}\right>\), \(E_\mathrm{I}\) is the CDFT energy of state \(\mathrm{I}\), and \(\mathbf{W}_c^\mathrm{AB}\) are the weight function matrices defined by
In the above expressions, capital subscripts have been used to emphasize the fact that the CDFT determinants are in general nonorthogonal. The electronic couplings and overlaps are collected into matrices \(\mathbf{H}\) and \(\mathbf{S}\), respectively. The off-diagonal elements of \(\mathbf{H}\) are not symmetric. The matrix is converted to symmetric form by setting
and setting \(\mathbf{H'}_\mathrm{BA}=\mathbf{H'}_\mathrm{AB}\).
The resulting matrix \(\mathbf{H'}\) is then orthogonalized to yield the final electronic coupling. The following orthogonalization methods are available:
Rotate CDFT states to eigenstates of the weight matrix \(\mathbf{W}\). This is the default behavior for systems with only one constraint that is identically defined across all CDFT states, not applicable otherwise.
Löwdin’s symmetrical orthogonalization \(\mathbf{H} = \mathbf{S}^{-1/2}\mathbf{H}'\mathbf{S}^{-1/2}\). This is the default behavior for systems with multiple constraints and can always be activated with the keyword LOWDIN.
The so-called wavefunction overlap method where the ground state Kohn-Sham solution is represented as the linear combination of CDFT states, see keyword WFN_OVERLAP.
Structure of input file
Mixed CDFT calculations are activated through the MIXED FORCE_EVAL section by setting MIXING_TYPE to MIXED_CDFT and providing an appropriate MIXED_CDFT input section. The individual CDFT states involved in a mixed CDFT calculation should correspond to different localizations of charge and/or spin in the same system. The constraint definitions do not have to be identical (i.e. defined using the same sets of atoms) in all states as long as the number of constraints is the same.
The CDFT states are included as their own FORCE_EVAL sections. It is
highly recommended that the CDFT states are first converged in separate simulations, the
FORCE_EVAL sections from these simulations are then copy-pasted into the
mixed CDFT input file, and the mixed CDFT method is used as post-processing analysis tool. The
converged wavefunctions and constraint strengths \(\vec\lambda\) should be supplied as restart
quantities for the mixed CDFT calculation. Using templates and the CP2K @include and @set
directives is strongly encouraged to keep the mixed CDFT input tidy, see the example input file
below
&FORCE_EVAL
METHOD MIXED
&MIXED
MIXING_TYPE MIXED_CDFT
NGROUPS 1
&MIXED_CDFT
! Calculate mixed CDFT properties every COUPLING step
COUPLING 1
! Settings determining how forces are mixed
FORCE_STATES 1 2
LAMBDA 1.0
! Orthogonalize CDFT states using Lowdin's method
! in addition to standard method
LOWDIN TRUE
! Configuration interaction?
CI FALSE
! Turn on printing
&PRINT
&PROGRAM_RUN_INFO ON
&END
&END PRINT
&END MIXED_CDFT
&END MIXED
@include subsys.inc
&END FORCE_EVAL
# Zn+ Zn
&FORCE_EVAL
@SET WFN_FILE ${WFN_FILE_1}
@SET RESTART ${RESTART_1}
@SET NAME ${PROJECT_NAME}-state1
@SET BECKE_TARGET ${BECKE_TARGET_1}
@SET BECKE_STR ${BECKE_STR_1}
METHOD QS
@include ${DFT_FILE}
&END FORCE_EVAL
# Zn Zn+
&FORCE_EVAL
@SET WFN_FILE ${WFN_FILE_2}
@SET RESTART ${RESTART_2}
@SET NAME ${PROJECT_NAME}-state2
@SET BECKE_TARGET ${BECKE_TARGET_2}
@SET BECKE_STR ${BECKE_STR_2}
METHOD QS
@include ${DFT_FILE}
&END FORCE_EVAL
In the above example input file, a common file ${DFT_FILE} is used as a template for the
DFT subsection. The CDFT state specific constraint settings and the
wavefunction filename are passed through variables. The electronic coupling is calculated using the
default weight function matrix and Löwdin orthogonalization methods. If molecular dynamics were
performed with the above input file, the forces would be mixed according to linear mixing scheme
\(F = \lambda F_1 + (1-\lambda) F_2\), where the states \(F_i\) are selected with the keyword
FORCE_STATES and the mixing parameter
\(\lambda\) with LAMBDA. No configuration
interaction calculation is performed. The MIXED_CDFT
section accepts some additional keywords, which have been described in the manual.
The keyword NGROUPS is set to 1, which implies that the two CDFT states are treated sequentially utilizing the full set of \(N\) MPI processes for the simulation. The CDFT weight function and its gradients are copied from state to state if the constraints definitions are identical in each CDFT state, because construction of these terms might be expensive in large systems.
The keyword NGROUPS could also be set to 2 or a larger value if using more than 2 CDFT states. In this case, each CDFT state is solved in parallel using \(N/N_\mathrm{groups}\) processors. This will likely reduce the wall clock time of your simulation at the expense of more computing resources. However, you should note that the weight function and its gradients are computed separately for each state instead of copied from state to state (if possible). This can be costly for large solvated systems.
A special run type is available for NGROUPS 2 if the keyword
PARALLEL_BUILD is activated. In this case,
the CDFT weight function and gradients are first built in parallel on \(N\) MPI processes, which are
subsequently copied onto the two MPI processor groups of size \(N/2\) which solve the CDFT states in
parallel. This operating mode is limited to two CDFT states with one identically defined total
charge density constraint. This operating mode is an advanced feature which might be useful for
large scale MD simulations to save computational wallclock time at the expense of higher CPU core
usage. The operating mode should only be used in conjuction with
dynamic load balancing if possible, and will likely
require tweaking the load balancing parameters.
Example: Electronic coupling of Zn cation dimer
In this example, we will calculate the electronic coupling for the reaction
\(\mathrm{Zn}^+ +\mathrm{Zn} \rightleftharpoons \mathrm{Zn}+ \mathrm{Zn}^+\). The initial and final
states of this reaction were already converged with CDFT in a
previous section of this tutorial. That part of the tutorial must be
completed before proceeding. The full input files, in particular the mixed CDFT input file
energy_mixed.inp, were also given in that section.
The converged CDFT states are used as input for the mixed CDFT calculation. The calculation does not
take long to run as a result. The mixed CDFT input file uses template files to keep the input tidy,
as was discussed in the previous section. Find and study the corresponding section in the
energy.bash script file to see how variables in the main mixed CDFT template energy_mixed.inp
are initialized.
A number of files are generated by the mixed CDFT calculation. The main output from the calculation
can be found in the file Zn-5A-mixed-cdft.out. The relevant part of the output is included below.
The mixed CDFT analysis is printed after the header lines MIXED_CDFT|. For each unique CDFT state
permutation \(\{i,j\}, i<j\), the constraint information is first summarized, the overlap and charge
transfer energies are printed, and the calculated electronic coupling(s) (and possibly other
quantities) are outputted. Here, both tested orthogonalization methods yield an electronic coupling
of 5.67 mHa, in agreement with the 5.49 mHa estimate from
the more expensive wavefunction based method CASSCF/MRCI+Q.
MIXED_CDFT| Activating mixed CDFT calculation
MIXED_CDFT| Number of CDFT states: 2
MIXED_CDFT| CDFT states calculation mode: serial
MIXED_CDFT| Becke constraint is built before the SCF procedure of the first
CDFT state and subsequently copied to other states
MIXED_CDFT| Calculating electronic coupling between states: T
MIXED_CDFT| Calculating electronic coupling reliability metric: F
MIXED_CDFT| Configuration interaction (CDFT-CI) was requested: F
MIXED_CDFT| Block diagonalizing the mixed CDFT Hamiltonian: F
MIXED_CDFT| Dynamic load balancing enabled: F
MIXED_CDFT| Matrix inversions calculated with LU decomposition.
------------------------- CDFT coupling information --------------------------
Information at step (fs): 0.00
############################################
###### CDFT states I = 1 and J = 2 ######
############################################
Atomic group: 1
Strength of constraint I: 0.371415167271
Strength of constraint J: -0.378315361740
Final value of constraint I: 11.000125488935
Final value of constraint J: 11.999828674539
Overlap between states I and J: 0.030261294466
Charge transfer energy (J-I) (Hartree): 0.000739539045
Diabatic electronic coupling (rotation, mHartree): 5.674875246867
Diabatic electronic coupling (Lowdin, mHartree): 5.674714192287
------------------------------------------------------------------------------
NO FORCE_EVAL section calculated the dipole
ENERGY| Total FORCE_EVAL ( MIXED ) energy (a.u.): -120.612670921735003
Other files created during the execution are related to the individual CDFT states. The *-r-1.out,
*-r-2.out, … files are the main output files for the CDFT simulations of the studied states.
Because preconverged solutions were employed, these CDFT simulations terminate immediately after the
first SCF step, and any matrices that are subsequently needed in the mixed CDFT analysis are stored
in memory. In the input file, the full project name and CDFT state ID number were stored in the
variable ${NAME} on a per state basis. This variable was used to prepend the name of any other
output files (e.g. the cdftLog files) that are created during the CDFT simulation of the individual
CDFT states. The output files from different CDFT states are therefore straightforward to
distinguish. The content of the additional files was discussed in a
previous section.
Example: Configuration interaction calculations with CDFT (CDFT-CI): The case of \(\mathrm{H}_2^+\)
DFT exchange-correlation functionals suffer from varying degrees of self-interaction error (SIE). A pathological example of a system where SIE leads to unphysical results with DFT is the simple dissociation reaction
\(\mathrm{H}_2^+ \rightarrow \mathrm{H}^+ + \mathrm{H}\).
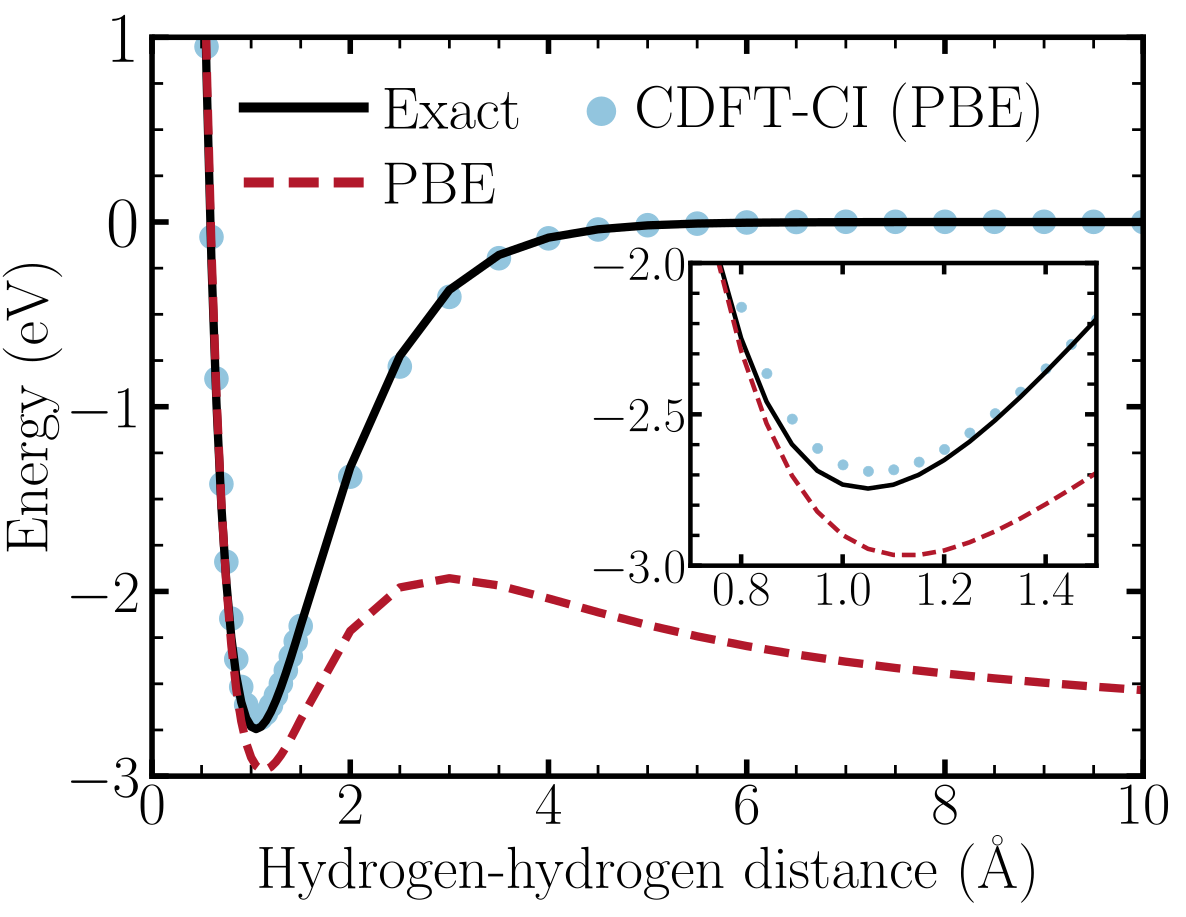
Even though this system contains only 1 electron, the dissociation profile obtained with PBE notably deviates from the exact Hartree-Fock profile as shown in Figure 4 below.
Figure 4. Illustration of DFT self-interaction error for the reaction \(\mathrm{H}_2^+ \rightarrow \mathrm{H}^+ + \mathrm{H}\). PBE notably deviates from the exact Hartree-Fock dissociation profile. The correct profile can be recovered with constrained DFT configuration interaction (CDFT-CI) using fragment constraint states \(|\mathrm{H^+H}>\) and \(|\mathrm{HH^+}>\) as the basis.
We can use CDFT states as the basis of a configuration interaction (CI) simulation to correct for SIE in this system. As the figure above shows, CDFT-CI using the PBE functional is able to reproduce the exact dissociation profile. You can read up on the theory behind CDFT-CI simulations from the references given at the start of this tutorial. Very briefly, CDFT-CI simulations involve representing the system’s wavefunction as a linear combination of multiple CDFT states where the charge/spin density is constrained differently in different states. The CI expansion coefficients and energies are then obtained by solving a generalized eigenvalue equation where the effective Hamiltonian matrix describes how the CDFT states interact with each other.
In this tutorial, you will reproduce the DFT and CDFT results from the figure above. You can find the input files here. The reference data used to plot Figure 4 are also included in the zip-folder. Please note that the reference results were obtained with a larger basis set and planewave cutoff as well as tighter convergence criteria than the settings you will be using in this tutorial.
Start by examining the simulation script
energy.bash. This tutorial involves a rather large number of simulations so running them will take a while. You can use the flag-xto separately run the different types of simulations (DFT, CDFT, CDFT-CI) needed in this tutorial.While the CDFT simulations are running, look at the results from the DFT simulations with PBE. Can you figure out the reason why PBE predicts an unphysical dissociation profile? (Hint. Compute the partial charges).
Inspect the output files produced by the CDFT-CI simulations once they are done. Find the output from the CDFT-CI module in the main output files. Look at the CI expansion coefficients in terms of the CDFT states. How would you characterize the CI wavefunction? Is the result sensible? What about the atomic partial charges in different CDFT states as a function of distance?
Plot the CDFT-CI and DFT dissociation profiles with your favorite plotting tool. Use the Hartree-Fock data from the provided data file as a reference. You can produce a similar data file from your simulations by calling
energy.bashwith the flag-x results.