Image Charges
Introduction
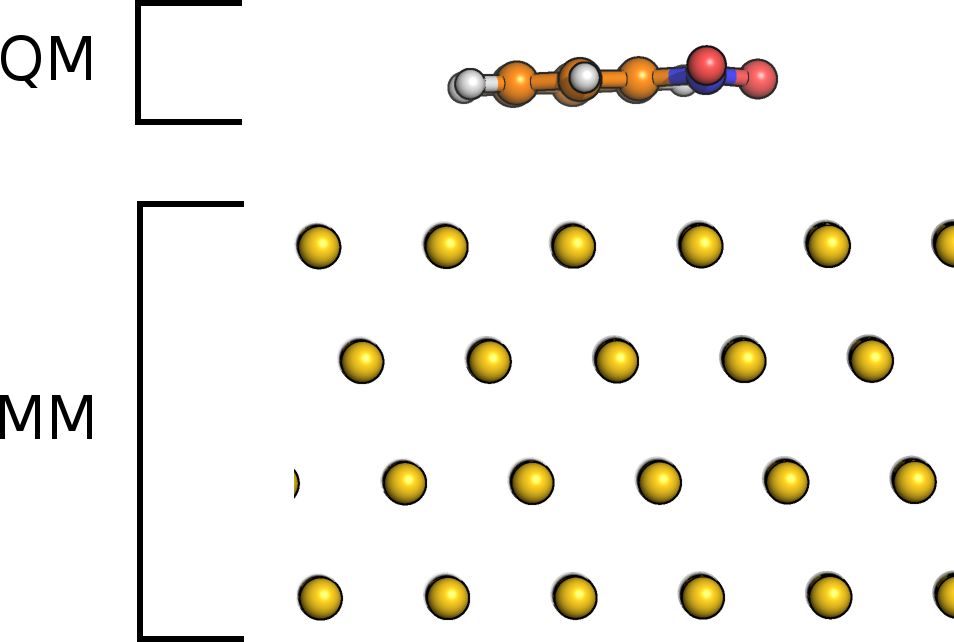
The image charge (IC) augmented QM/MM model in CP2K is designed for the simulation of adsorbate-metal systems. The adsorbate is treated by QM whereas the metallic substrate is described by classical force fields.
Figure: Nitrobenzene molecule on Au111. Separation in subsystems for IC-QM/MM.
The interactions between metal and adsorbate are described at the MM level of theory accounting for the polarization of metal and adsorbate by an IC approach. The charge distribution \(\rho_m\) in the metal is modeled by a set of Gaussian charges (image charges) centered at the metal atoms,
where \(\mathbf{R}_\mathrm{a}\) is the position of metal atom \(a\) and \(g_a\) the spherical Gaussian function located at \(a\). The expansion coefficients \(c_a\) are unknown and determined in a self-consistent procedure imposing the constant-potential condition within a metal, i.e. the sum of \(V_H(\mathbf{r})\) generated by the charge density \(\rho(\mathbf{r})\) of the molecule and \(V_m(\mathbf{r})\) generated by \(\rho_m\) has to be constant within the metal,
In this expression \(V_0\) is a constant potential that can be different from zero, if an external potential is applied. The implementation is embedded in the Gaussian and plane waves scheme of CP2K and thus naturally suited for periodic systems. Details of the theory and implementation are described in Golze2013.
Basic input
The IC method is specified in the QMMM section by
&QMMM
:
:
&IMAGE_CHARGE
MM_ATOM_LIST 1..576
EXT_POTENTIAL 0.0
&END IMAGE_CHARGE
&END QMMM
The keyword MM_ATOM_LIST defines the list of MM atoms that carrying an image charge. These are typically all metal atoms. EXT_POTENTIAL corresponds to \(V_0\) above and is set to 0.0V by default. Note that the QM and MM box must have the same size for an IC-QM/MM calculation.
Print options
Detailed energy information and the normalized IC coefficients \(q_a\) can be printed out by IMAGE_CHARGE_INFO. The normalized IC coefficients are defined as \(q_a = c_a\left(\frac{\alpha}{\pi}\right)^{-\frac{3}{2}}\), where \(\alpha\) is the width of the Gaussian.
&QMMM
:
:
&PRINT
&IMAGE_CHARGE_INFO
&END
&END PRINT
&END QMMM
Advanced input options
Additional keywords that can be set in IMAGE_CHARGE are:
&IMAGE_CHARGE
MM_ATOM_LIST 1..576
EXT_POTENTIAL 0.0
WIDTH 3.5
IMAGE_MATRIX_METHOD MME
DETERM_COEFF CALC_MATRIX
RESTART_IMAGE_MATRIX .false.
&END IMAGE_CHARGE
WIDTH refers to the width \(\alpha\) of the Gaussian \(g_a\), which is the only adjustable parameter in our IC model. The energies and gradients do not depend on \(\alpha\) for values larger than 3.0 Å\(^{-2}\). Small values of \(\alpha\) correspond to very broad Gaussians, which will lead to technical artifacts. Extremely large values are not recommended, too.
IMAGE_MATRIX_METHOD determines how
the IC matrix \(T_{ab}\), Eq. 11 in Golze2013, is calculated. GPW corresponds to the algorithm
shown in Fig. 1 in J. Chem. Theory Comput., 9, 5086 (2013), whereas MME is an integral scheme that
has been recently implemented and that is significantly faster.
DETERM_COEFF specifies how the expansion
coefficients \(c_a\) are determined. With CALC_MATRIX, \(T_{ab}\) is calculated and the linear set of
equations is solved. ITERATIVE avoids calculation of \(T_{ab}\) in each SCF step by using an
iterative conjugate gradient scheme. The new integral scheme MME evaluates the matrix \(T_{ab}\)
very quickly, i.e. the iterative solutions is not required here, thus set always CALC_MATRIX.
RESTART_IMAGE_MATRIX can be used to
restart \(T_{ab}\) for an MD simulation if ITERATIVE is set.
Note
Setting these additional keywords is typically not required. The default settings are fine.
Typical setup
The typical setup for an IC-QM/MM simulation is as follows
adsorbed molecules described by DFT
metal is constrained or described by an embedded atom model (EAM)
Interactions between QM and MM:
Pauli repulsion, dispersion etc. modeled by force fields e.g. Lennard Jones
electrostatic interaction/induction: IC model
Example input files
The first input example is a single guanine molecule on an Au111 surface using a modified Born-Mayer potential to describe Pauli repulsion and dispersion between molecule and metal. The second example is a single water molecule on Pt111. The interactions between water and metal are modeled by the Siepmann-Sprik potential, see Siepmann1995.
Guanine@Au111: Au111_guanine
H2O@Pt111: Pt111_1H2O